🎨

Computer Graphics

2024 — C++ and OpenGL Fundamentals

About

Learning computer graphics from the ground up with C++ and OpenGL/GLUT. From basic 2D shapes to 3D transformations, exploring the mathematics that powers visual computing.

🖼️ Rendered Examples

3D Cube

3D Colored Cube

Depth buffering, perspective projection, edge rendering, and per-face coloring

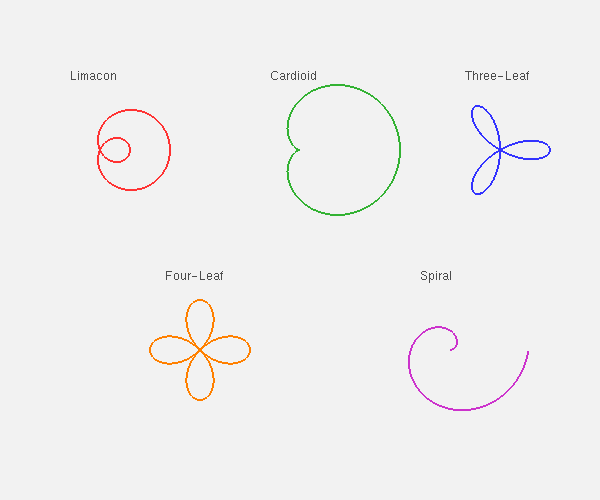
Mathematical Curves

Mathematical Curves

Limacon, Cardioid, Three-Leaf, Four-Leaf, and Spiral using polar equations

Polygons

Regular Polygons

From triangle to circle — filled shapes with outlines

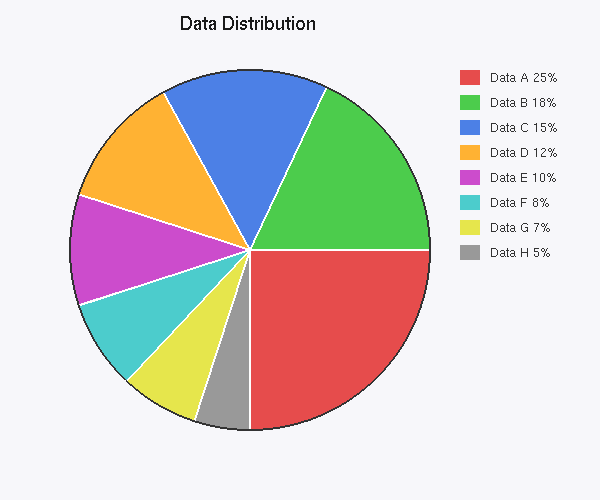
Pie Chart

Data Visualization

Pie chart with dynamic slices, labels, and legend

Topics Covered

📐 2D Graphics

  • • Basic shapes: lines, triangles, polygons
  • • Mathematical curves (polar coordinates)
  • • Transformations: translate, rotate, scale
  • • Filled polygons with vertex colors

🧊 3D Graphics

  • • 3D primitives: cubes, spheres
  • • Perspective and orthographic projection
  • • Depth buffering (Z-buffer)
  • • Model-View-Projection matrices

🎨 Advanced Topics

  • • Bezier curves and surfaces
  • • Filled hexagons and complex polygons
  • • Animation with timer callbacks
  • • Double buffering for smooth rendering

📊 Data Visualization

  • • Pie charts with 3D perspective
  • • Color mapping and gradients
  • • Interactive viewports

Code Sample: Drawing a Cube

// Set up 3D view
glTranslatef(0.0, 0.0, -5.0);
glRotatef(30, 1.f, 1.f, 0.f);

// Draw cube faces with colors
glBegin(GL_QUADS);
  // Front face - Green
  glColor3f(0.0f, 1.0f, 0.0f);
  glVertex3f(-0.5f, -0.5f, 0.5f);
  glVertex3f( 0.5f, -0.5f, 0.5f);
  glVertex3f( 0.5f,  0.5f, 0.5f);
  glVertex3f(-0.5f,  0.5f, 0.5f);
  // ... more faces
glEnd();

Mathematical Curves

Curves generated using polar coordinate equations:

Limacon: r = a·cos(θ) + b
Cardioid: r = a·(1 + cos(θ))
Three-Leaf: r = a·cos(3θ)
Four-Leaf: r = a·cos(2θ)
Spiral: r = a·θ

Tech Stack

C++ OpenGL GLUT GLU Linear Algebra

What I Learned

  • • The graphics pipeline: vertex → transformation → rasterization → fragment
  • • Matrix math for 3D transformations (translate, rotate, scale, project)
  • • How GPUs use parallel processing for rendering
  • • Double buffering to prevent screen tearing
  • • Depth testing to handle occlusion in 3D scenes
View Source Code
← Back to Journey